「多段階人口波動曲線」を1996年に提唱して以来、より説得的な論拠を探してきましたが、ほぼ10年をかけて、新たな手法を見つけました。
超長期的な人口推移を「逆対数×正対数」のグラフにすることで、さらに明確な波動をとらえることができたのです。
前回紹介したJ-N.Birabenの「世界人口推移グラフ」では、縦軸だけの片対数グラフとなっていました。このグラフから読み取ったデータで、改めて縦対数尺のグラフを作成してみると、下図のようになります。
Birabenがこうしたグラフを描いた意図は、次のように推測されます。
古い時代の人口推移は、①母集団の数が少ない、②平均寿命が短い、などの理由で、比較的ゆっくりと微妙な変化を示します。一方、新しい時代の推移は、①母集団の数が次第に大きくなる、②平均寿命が徐々に長くなる、などの理由で、比較的短期間に大きな変化を示します。
そこで、縦軸に対数をとれば、古い時代の変化は拡大し、新しい時代の変化は縮小しますから、長期的な人口推移の大まかな波を抽出できるのです。
確かにこのグラフを見ると、人口の長期的な増減が鮮やかに浮上しています。
しかし、-5000年以前の推移が比較的ゆっくりと動いているのに対し、それ以降の推移は急速に増減を繰り返しています。これでは、近時点の微妙な変化を把握することはできません。
そこで、筆者は横軸も対数尺、それも逆対数の両対数グラフを採用してみました。新しい時代はゆっくりと、古い時代は短くとらえたいと思ったからです。
古い時代の人口推移については、量的な変化は拡大、時間的な変化は短縮し、新しい時代の推移については、量的な変化は縮小、時間的な変化は延長して描く、という方法を採用したのです。
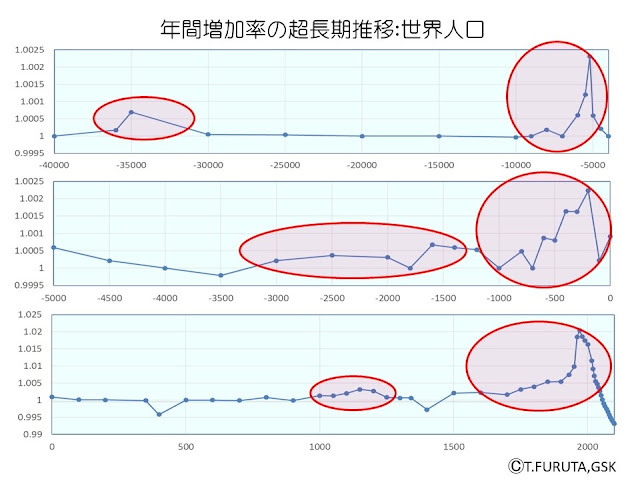
こうした手法で新たに描いたのが、下図のような「横軸:逆対数、縦軸:正対数」のグラフです。
いかがでしょうか? これを一目見れば、世界人口の超長期的推移には、5つの波があったことが、どなたにでもはっきりと読み取れるでしょう。
これこそ、筆者の提唱する「人口波動」です。超長期的な人間の個体数変化には、間違いなく5つの波があったのです。
文献やサイトなどで調べてみたのですが、こうした発想は、先達の業績にはまったく見つかりませんでした。その意味では、おそらく世界で初めて人口波動を確認したものともいえるでしょう。
これによって、マルサスが『人口論・第6版』(1826年)で初めて提唱した「人口の長期的推移は波を打つ」という視点、つまり「オシレーションズ(Oscillations)」(擺動、波動と翻訳)という理論的仮説を、ともかくも実証することができたと思います。
「この種の擺動はおそらく普通の人にははっきりと見えないであろう。そして最も注意深い観察者にとってすら、その時期を計ることは困難であろう」と述べていたマルサスの波動が、誰にでも見分けられるのです。
グラフの初出は『日本人はどこまで減るか』(2008年)であり、その改良版は「5つの人口波動から解く、日本の人口が浮上する条件」(『人の死なない世は極楽か地獄か』所収、2011年)や「人口減少社会の背景と展望」(統計研究会『ECO-レポート』(2015年1月号)に載せています。
さらにいえば、「横軸:逆対数」という発想は、単にグラフを作成する上での改良に尽きるものではありません。
それを超えて、人類の歴史を振り返る時には、古い時代の微量かつ長期の変化は圧縮し、新しい時代の大量かつ短期の変化は拡大して考えるべきだ、というパラダイムそのものの転換を意味しているからです。